딥러닝 신경망 - (3) 신경망 연산, ReLu 함수
이번 글은 딥러닝 연구를 위한 신경망 세 번째 글인 신경망 연산과 relu 함수에 대해서 다루도록 하겠습니다.
기본적인 자료는 프랑소와 솔레가 저술한 ‘케라스 창시자에게 배우는 딥러닝(길벗)’ 서적의 내용을 토대로 따왔으며, 제가 직접 그린 이미지도 있지만 책의 이미지도 일부 따왔음을 먼저 알려드립니다. 이번 글은 상기 서적의 2장을 다루었으나, 책의 내용을 참고하여 제 기준에서 나름대로 정리한 내용입니다. 너무 많은 내용을 자세히 설명하면 저작권에 문제가 될 소지가 있으므로 구체적으로는 다루지 않고 대략적으로만 다루니 양해 바랍니다.
본문에 있는 코드 중 일부는 해당 책의 코드이고, 일부는 제가 임의로 작성한 코드이니 역시 참고 바랍니다.
신경망 연산
신경망 연산이라. 듣기만 해도 머리가 아프겠죠?
사실 책에서는 각 알고리즘에 대한 구성이나 내용 등등을 설명하고 그랬는데, 글쎄요. 굳이 그럴 필요가 있을까 싶기도 하고 그렇습니다. 개념만 알고 어떤 식으로 변경되는지만 알면 그만인데, 수학 공식에 대입하고 어쩌고. 머리아픕니다.
그래서 실제 연산 관련해서는 개념 중심으로만 다루도록 하겠습니다.
앞서 첫 번째 글에서 나타낸 MNIST 모델에 대한 예제 코드는 다음과 같았습니다.
from keras.datasets import mnist
from keras import models, layers
from keras.utils import to_categorical
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
network = models.Sequential()
network.add(layers.Dense(512, activation='relu', input_shape=(28*28,)))
network.add(layers.Dense(10, activation='softmax'))
network.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy'])
train_images = train_images.reshape((60000, 28*28))
train_images = train_images.astype('float32') / 255
train_labels = to_categorical(train_labels)
network.fit(train_images, train_labels, epochs=5, batch_size=128)이제 예제 코드를 이해하기 위해서 하나씩 살펴보도록 하겠습니다.
일단 각 코드가 무엇을 하는 지에 대해서는 지난 글을 통해서 대략적으로 설명한 바 있었습니다.
- 훈련 모델, 테스트 모델을 생성하고
- 층을 하나씩 생성하고
- 층에 입력할 수 있는 형태로 모델 형태를 변경하고
- 실제 입력하고
사실 훈련 모델, 테스트 모델 생성과 관련해서 추가적으로 할 말은 없습니다. 단순한 변수 대입이기 때문입니다.
다음은 층을 생성하는 부분입니다. network.add()를 사용하여 신경망 층을 생성하죠. 신경망 층은 layers.Dense()를 사용합니다.
이제 layers.Dense()가 무엇인지를 자세히 설명해야겠죠.
layers.Dense()는 어떤 신경망을 생성할 것인지를 결정하는 부분으로, 첫 번째 층에서는 relu 함수를 사용해서 신경망을 생성하겠다고 하였습니다. 그렇다면 relu 함수가 무엇인지에 대해서는 한 번 알아두도록 합시다. 실제로 매우 자주 쓰이는 함수인 만큼 미리 알아두는 것이 좋겠죠.
Keras의 Layer에서 relu함수가 어떤 형태로 연산되는지를 한 번 파악한다면 다른 함수를 사용하는 것도 방법의 차이만 있을 뿐 어렵지 않게 이해할 수 있을 것입니다.
relu
relu는 ReLu라고 대소문자 쓰고요. Rectified Linear Unit이라고 합니다. 간단히 말하자면 이런 겁니다.
y = max(x, 0)
이게 relu입니다. 입력값이 0보다 크면 그 값이 나오고, 0보다 작으면 0으로 나타납니다.
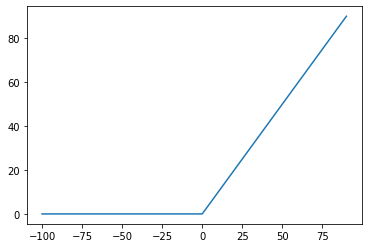
relu 함수는 다음과 같은 식을 따릅니다.
output = relu(dot(W, input) + b)- input과 output은 당연히 입력과 출력이겠죠.
- W하고 b는 가중치(Weight)와 편향(Bias)를 나타냅니다.
- dot은 점곱(dot operation)을 나타냅니다. 점곱에 대해서는 아래에서 자세히 설명하겠습니다.
그런데 우리는 가중치와 편향을 알 수는 없고, 이를 임의로 설정할 수도 없습니다. 그저 저 값들은 자동으로 생성됩니다. 생성 방식은 임의의 작은 난수 형태로 생성되며(무작위 초기화(random initialization)), 연산을 수행할 때마다 input의 값에서 output이 나타나도록 가중치와 편향을 자동으로 조절하는 형태로 이루어집니다.
그 외에도 인자값으로 512, input_shape=(28*28,)이 들어갑니다.
여기서 첫 번째 인자인 512는 은닉 유닛(hidden units)의 개수를 설정하는 부분으로, 여기에서는 ‘차원’이라는 용어를 사용합니다. 은닉 유닛이란 쉽게 말하면 입력과 출력 사이에 계산을 할 때 사용되는 유닛을 뜻합니다.
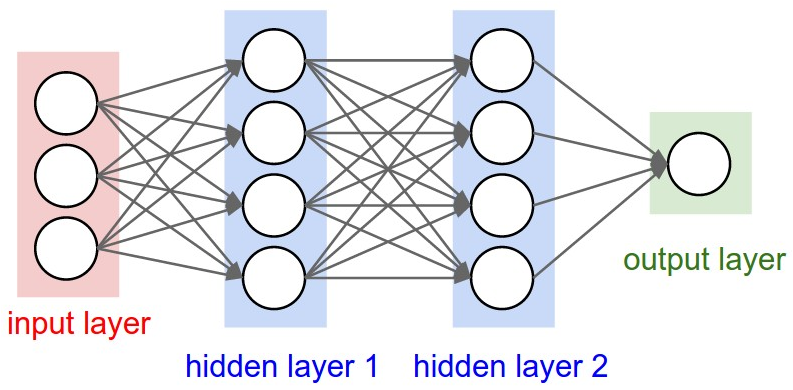
※ 출처: aikorea.org -
위 사진을 기준으로 한다면 Hidden layer가 은닉 유닛이 되며, 차원이 많을 수록 연산도 그만큼 많이 해서 더욱 자세하게 계산되겠죠.
다음은 input_shape입니다. 각 층 별로 연산을 하기 위해서는 입력되는 값도 층에서 요구하는 입력값과 일치해야 합니다. MNIST 모델은 실제로 60000 x 28 x 28 의 형태(Shape)로 구성되어 있으며, 여기서 60000은 이미지가 60000개라는 뜻이고, 28 x 28은 Width x Height를 나타냅니다.
train_images는 numpy 배열 형태 변수로 구성되어 있지만, 픽셀 하나하나에 대해서 연산을 수행해야 하기 때문에 28 x 28 형태의 배열이 아니라 28 * 28, 즉 784개의 픽셀에 대한 코드 값으로 나타냅니다. 그래서 아래쪽에 train_images.reshape((60000, 28*28))를 수행하여 28 x 28을 784로 변경하는 작업도 수행합니다.
train_images.reshape()를 수행한 한 개의 이미지에 대한 일부 예제입니다. (784개를 다 넣기엔 화면이 너무 차서 일부만 넣겠습니다)
0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0.2509804 0.7490196 0.5019608 0.
0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 1. 1. 1. 0.5019608
0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0.
0. 0. 0.7490196 1. 1. 1. 1.
0.7490196 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0.
0. 0.2509804 1. 1. 1. 1. 1.
1. 1. 0.7490196 0.5019608 0.7490196 0.7490196 1.
1. 0.7490196 0.2509804 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0.
0.2509804 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1.
1. 1. 0.5019608 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0.
0.7490196 1. 1. 0.5019608 0. 0. 0.2509804
0.7490196 1. 1. 1. 1. 1. 0.7490196
0.5019608 0.5019608 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0.2509804relu 함수는 위에서 언급했다시피 0보다 작을 때 0으로 설정하므로 train_images을 그대로 넣을 경우에는 아무런 값도 바뀌지 않습니다. 왜냐하면 train_images는 각 이미지 픽셀 별로 칼라 코드를 반환하는데, 칼라 코드는 0에서 255까지이고, float32 형태로 255를 나누기 때문에 실제 결과는 0에서 1 사이의 값을 나타내기 때문입니다.
하지만 가중치와 편향을 사용해서 조절한다면 0보다 작은 값이 나타날 수 있으며, 이 때 relu 함수의 결과로 0으로 변환이 되는 형태로 이루어집니다.
이제 점곱에 대해서 설명하겠습니다. 점곱은 간단히 행렬 간의 연산을 나타냅니다.
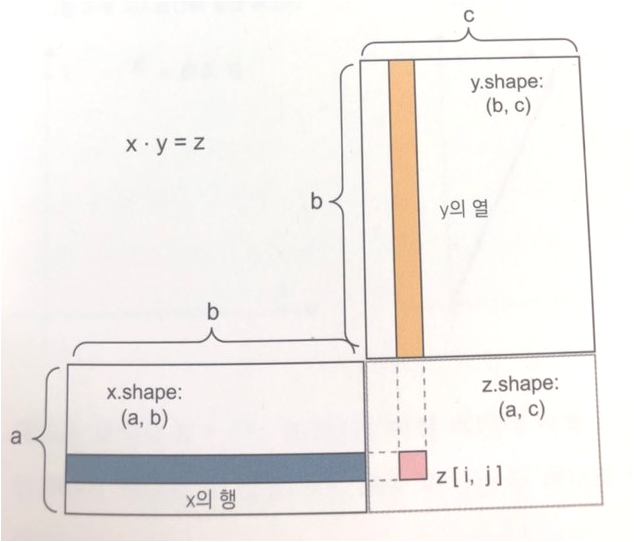
※ 출처: 상기 언급한 참고서적
좌측 하단 x.shape는 (2828,n)개가 됩니다. 여기서 n개는 몇 개인지는 모르지만, 한 번의 점곱을 수행할 때 2828=784개의 이미지 픽셀 데이터가 입력된다는 것을 의미합니다. n개를 설정하는 부분은 신경망에서 사전에 설정하지는 않습니다. x는 실제 입력을 나타내기 때문에, test_image를 가지고 훈련을 할 때 몇 개씩 훈련하겠다라는 부분을 지정하면(batch_size), 해당 사이즈만큼으로 설정됩니다.
우측 상단 y.shape는 (n,512)개가 됩니다. n개에 대한 부분은 이미 위에서 설명했으므로 생략하며, 512는 앞서 설명한 은닉 유닛의 차원을 나타냅니다. relu 함수가 512차원으로 되어있으므로 그에 해당되는 결과가 나타나겠죠.
다시 한 번 relu 함수의 식을 보겠습니다.
output = relu(dot(W, input) + b)위 내용을 종합해서 요약하면 매우 간단해집니다.
가중치 W와 입력값 input에 대한 점곱을 수행한 후 편향 B를 더한 다음, relu 함수를 수행하면 0보다 큰 값은 그대로 유지되는 반면, 0보다 작은 값은 0으로 치환되어 연산될 것입니다.
이 신경망에 대한 유효성 여부를 여기서 바로 알 수는 없습니다. 다만 앞에서 언급한 것처럼 무작위 초기화를 통해서 W와 B를 구한 다음, 이 값을 변경시켜나가는 형태로 진행될 예정입니다.
relu 함수를 사용한 신경망 층은 여기까지입니다. 꽤 설명이 길었지만, layers.Dense()에서 어떻게 함수가 작동되는지를 알기 위해서는 이러한 부분에 대한 설명은 필요할 것 같아서 쓰게 되었습니다. (사실은 제가 정리하기 위한 용도이지만)
신경망 연산 첫 번째 글은 여기서 마치겠습니다. 뒤의 연산에 대해서는 다음 글에 이어서 설명하겠습니다.
